che si riducono ad addizioni
che paiono diverse da quelle degli intelligibili su cui le dialettiche si
esercitano per prime, vedono la diversità assumere l'aspetto di una diminuzione
dei qualitativi che son membri dei polinomi, e che una certa descrizione dovrà
esser fornita, data la problematicità dell'intelligibile uno e sintetico, delle
operazioni e dei punti di applicazione delle operazioni delle dialettiche di
condizione umana, per la teoria platonica la comprensione di un intelligibile
verrà ancora ridotta a un polinomio in cui però il primo binomio è connessione
necessaria di più qualitativi equifunzionali al monomio qualitativo di partenza
ed è punto di articolazione di più qualitativi equifunzionali in nesso
necessario con esso, con la conseguenza che una comprensione sola avrà
qualificazione completa, quella in cui ogni qualitativo addizionato, ad
eccezione del primo, è in realtà una molteplicità di qualitativi
equifunzionali, mentre tutte le altre varieranno dalla prima per la
sostituzione alla molteplicità di un qualitativo addizionale di uno solo dei
qualitativi equifunzionali e per la conseguente eliminazione di tutti i
qualitativi equifunzionali che vanno aggiunti agli esclusi, e che un'altra
descrizione dovrà esser fornita per quelle operazioni e per quei loro punti di
applicazione - per una teoria aristotelica, essendo tutti i qualitativi, che è
dato assumere a biffe di dialettiche come parti ritrovate in un uno tutto, sia
pur problematico, e non come parti di parti, A B C D E F....Z, si avranno
intelligibili a comprensioni qualificate da un polinomio a massimo numero di
monomi qualitativi e intelligibili altri da questi per la loro comprensione qualificata
da un polinomio i cui monomi sono gli stessi del primo ma diminuiti di uno o
più qualitativi, essendo la formula dei primi X ={[([{ A.B }.F].L).O]. Z}, in
cui B è biffa con A di uno spostamento d'attenzione a nesso apodittico, F biffa
con {A. B } di identico spostamento e lo stesso L con [{ A.B }.F] e O con
([{A.B }.F].L) e Z con [([{A.B}.F].L).O], essendo la formula degli altri Y=([
{A.B}.F].L), in cui ogni monomio addizionato è biffa con gli altri secondo la
stessa forma; per una teoria platonica, essendo tutti i qualitativi che son
biffe di dialettiche come parti di un tutto e non come parti di parti, gli
stessi di cui sopra, si avrà un intelligibile solo con comprensione costituita
da un polinomio a massimo numero di monomi qualitativi, numero espresso dalla
totalità dei qualitativi e si avranno le comprensioni degli altri intelligibili
costituite da polinomi a minor numero di qualitativi, essendo la formula del
primo
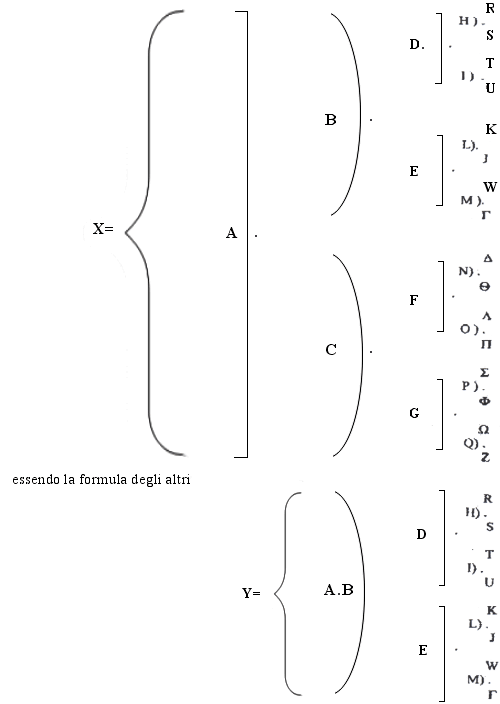
e la formula di quello a comprensione minima Y (psi) =[{ ([A.B].D).H}.R], con spostamenti d'attenzione da ogni qualitativo a quelli cui necessariamente è legato identici agli altri -; ora, sia nel caso che una dialettica acquisti intelligibilità grazie al rilievo dato alla necessità dello spostamento d'attenzione che la costituisce da uno dei qualitativi denotanti la comprensione o a un altro o a un binomio o polinomio di altri della stessa comprensione, sia nel caso che una dialettica acquisti intelligibilità per la necessità con cui il suo spostamento d'attenzione segue e rende autocosciente l'immanenza qualitativo-funzionale di una denotante qualitativa nella totalità del polinomio della sua comprensione o la stessa immanenza della stessa denotante nelle totalità dei vari polinomi di tutte le comprensioni in cui la denotante immane -ad esempio, nei rispettivi giudizi: la razionalità è connessa necessariamente alla mammiferinità (o giudizi verbali diversi ma indici della stessa